Тригонометрические функции
Синус
Уравнение y = sin x, график - синусоида
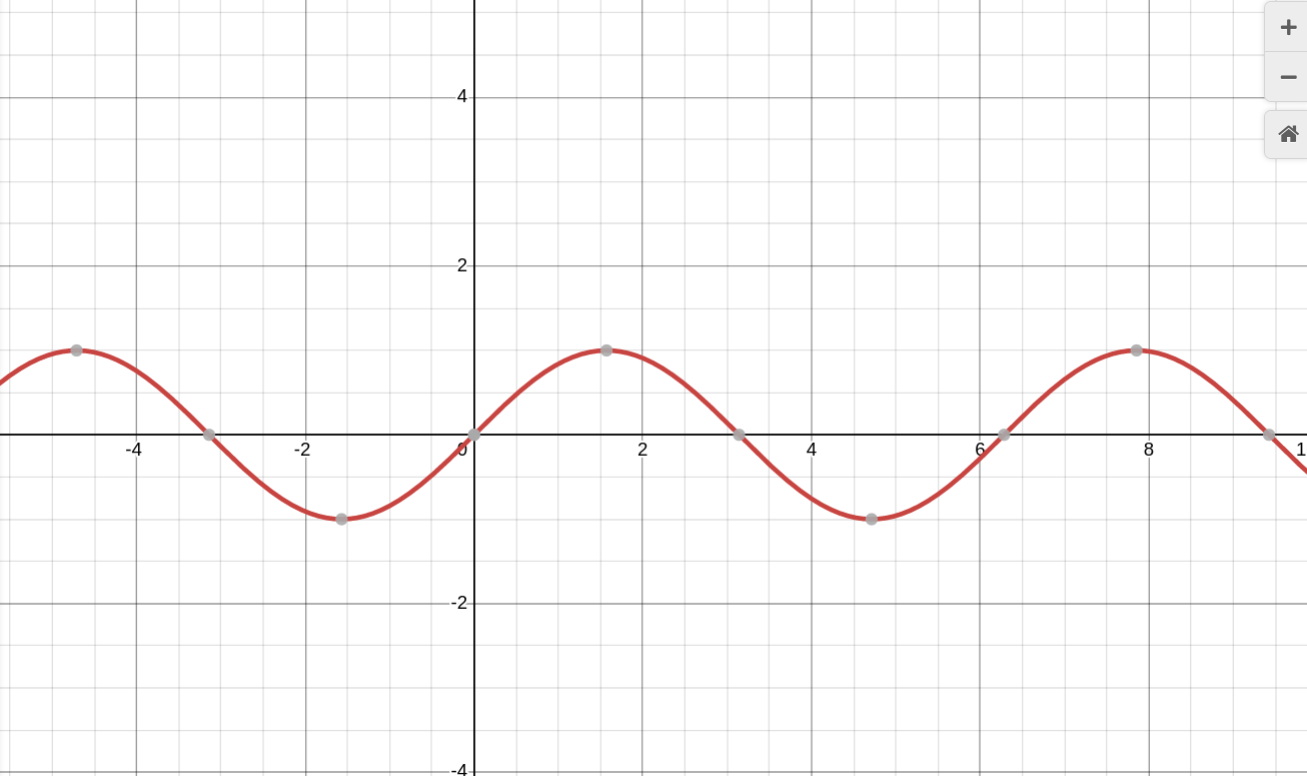
Свойства:
1. Область определения: D(y) = R
2. Область значений: E(y) = [−1; 1]
3. Функция нечётная: sin(−x) = −sin x
4. Функция периодическая с периодом 2π
5. Точки пересечения с осями координат:
Ox: (πk; 0), k ∈ Z;
Oy: (0; 0)
6. Промежутки знакопостоянства:
sin x > 0 при x ∈ (2πk; π + 2πk), k ∈ Z
sin x < 0 при x ∈ (π + 2πk; 2π + 2πk), k ∈ Z
7. Промежутки возрастания и убывания:
возрастает на промежутках x ∈ [−π/2 + 2πk; π/2 + 2πk], k ∈ Z
убывает на промежутках x ∈ [π/2 + 2πk; 3π/2 + 2πk], k ∈ Z
8. Максимумы и минимумы:
наибольшее: sin x = 1 при xmax = π/2 + 2πk, k ∈ Z
наименьшее: sin x = −1 при xmin = −π/2 + 2πk, k ∈ Z
Смещение, растяжение, сжатие
y = A sin(bx + c) + D
При b > 1 график сжимается по оси Ox в b раз, при 0 < b < 1 график растягивается по оси Ox, при b < 0 график отражается относительно оси Oy
При A > 1 график растягивается по оси Oy в A раз, при 0 < A < 1 график сжимается по оси Oy, при A < 0 график отражается относительно оси Ox
При c > 0 график смещается влево по оси Ox на c единиц, при c < 0 график смещается вправо по оси Ox
При D > 0 график смещается вверх по оси Oy на D единиц, при D < 0 график смещается вниз по оси Oy
Косинус
Уравнение y = cos x, график - синусоида
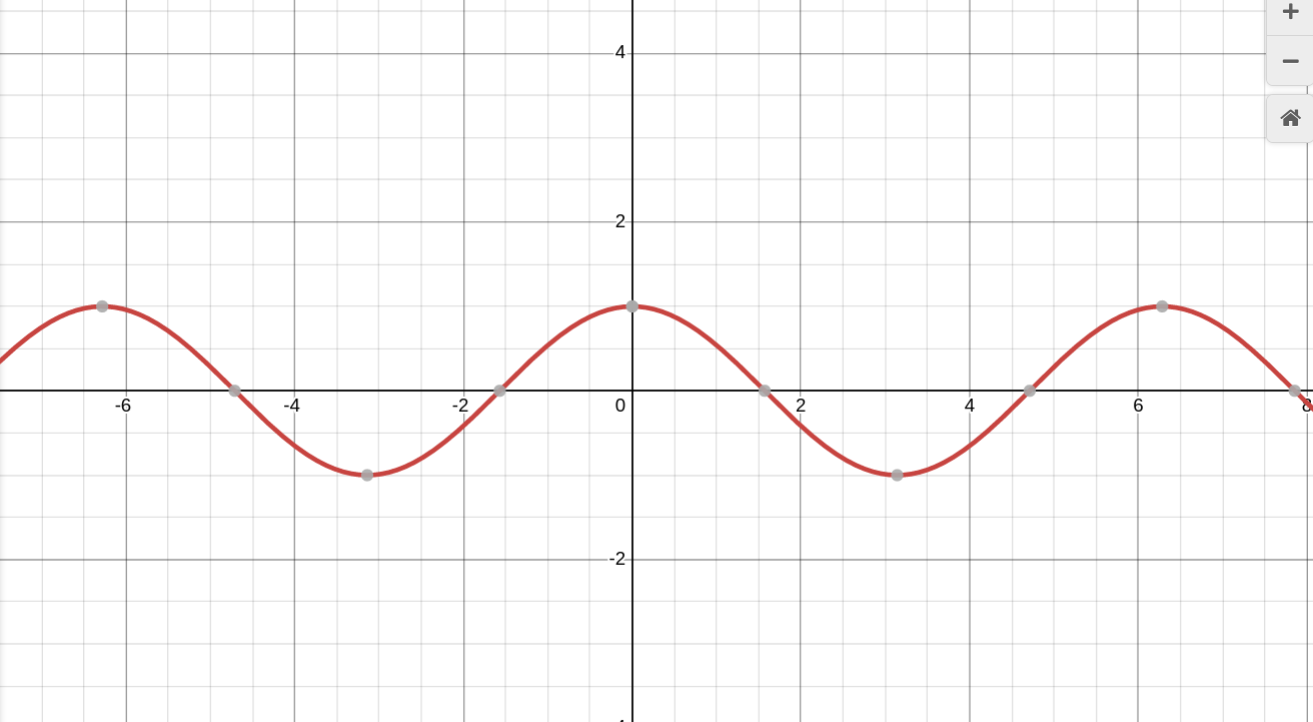
Свойства:
1. Область определения: D(y) = R
2. Область значений: E(y) = [−1; 1]
3. Функция чётная: cos(−x) = cos x
4. Функция периодическая с периодом 2π
5. Точки пересечения с осями координат:
Ox: (π/2 + πk; 0), k ∈ Z;
Oy: (0; 1)
6. Промежутки знакопостоянства:
cos x > 0 при x ∈ (−π/2 + 2πk; π/2 + 2πk), k ∈ Z
cos x < 0 при x ∈ (π/2 + 2πk; 3π/2 + 2πk), k ∈ Z
7. Промежутки возрастания и убывания:
возрастает на промежутках x ∈ [π + 2πk; 2π + 2πk], k ∈ Z
убывает на промежутках x ∈ [2πk; π + 2πk], k ∈ Z
8. Максимумы и минимумы:
наибольшее: cos x = 1 при xmax = 2πk, k ∈ Z
наименьшее: cos x = −1 при xmin = π + 2πk, k ∈ Z
Тангенс
Уравнение y = tg x, график - тангенцоидa
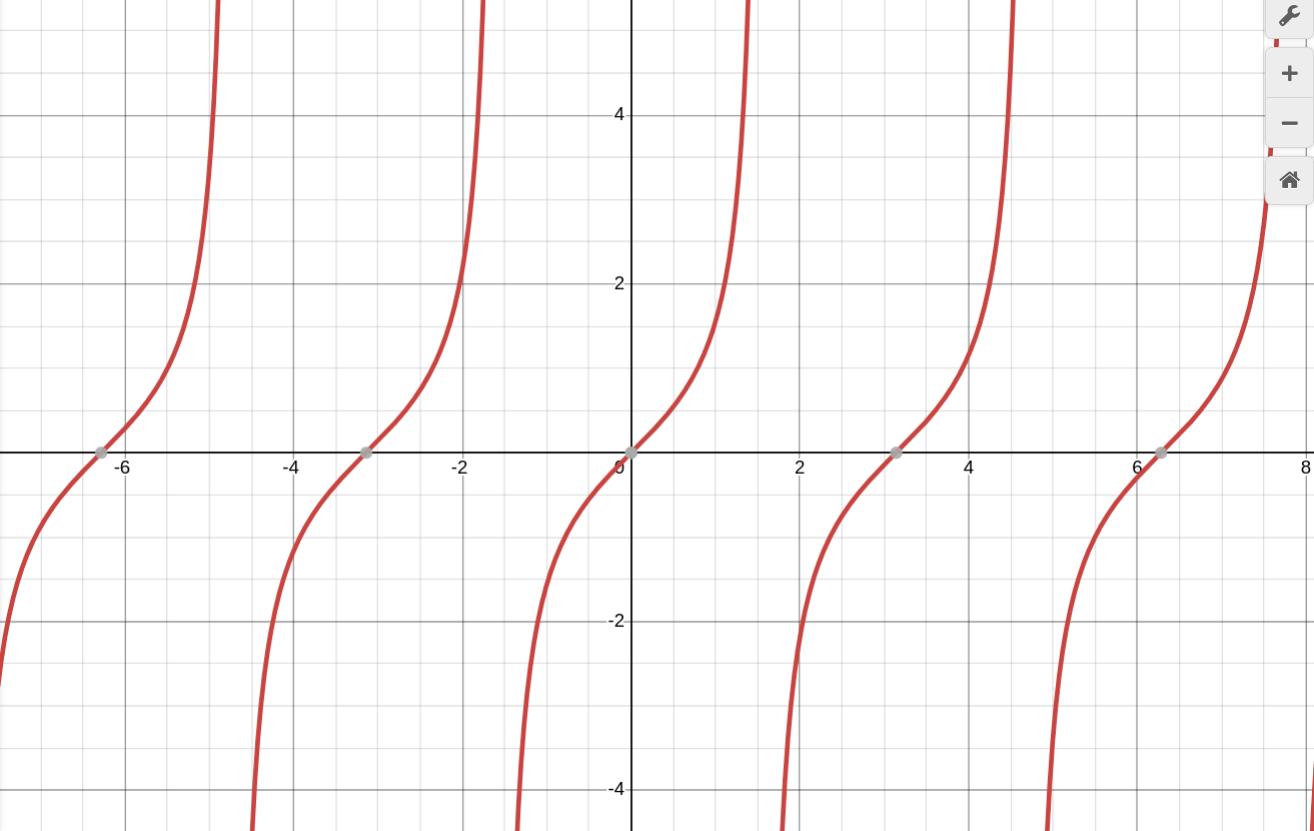
Свойства:
1. Область определения: x ≠ π/2 + πk, k ∈ Z
2. Область значений: E(y) = R
3. Функция нечётная: tg(−x) = −tg x
4. Функция периодическая с периодом π
5. Точки пересечения с осями координат:
Ox: (πk; 0), k ∈ Z;
Oy: (0; 0)
6. Промежутки знакопостоянства:
tg x > 0 при x ∈ (πk; π/2 + πk), k ∈ Z
tg x < 0 при x ∈ (π/2 + πk; π + πk), k ∈ Z
7. Промежутки возрастания и убывания:
возрастает на промежутках x ∈ (−π/2 + πk; π/2 + πk), k ∈ Z
8. Максимумы и минимумы: отсутствуют
Котангенс
Уравнение y = ctg x, график - тангенцоидa
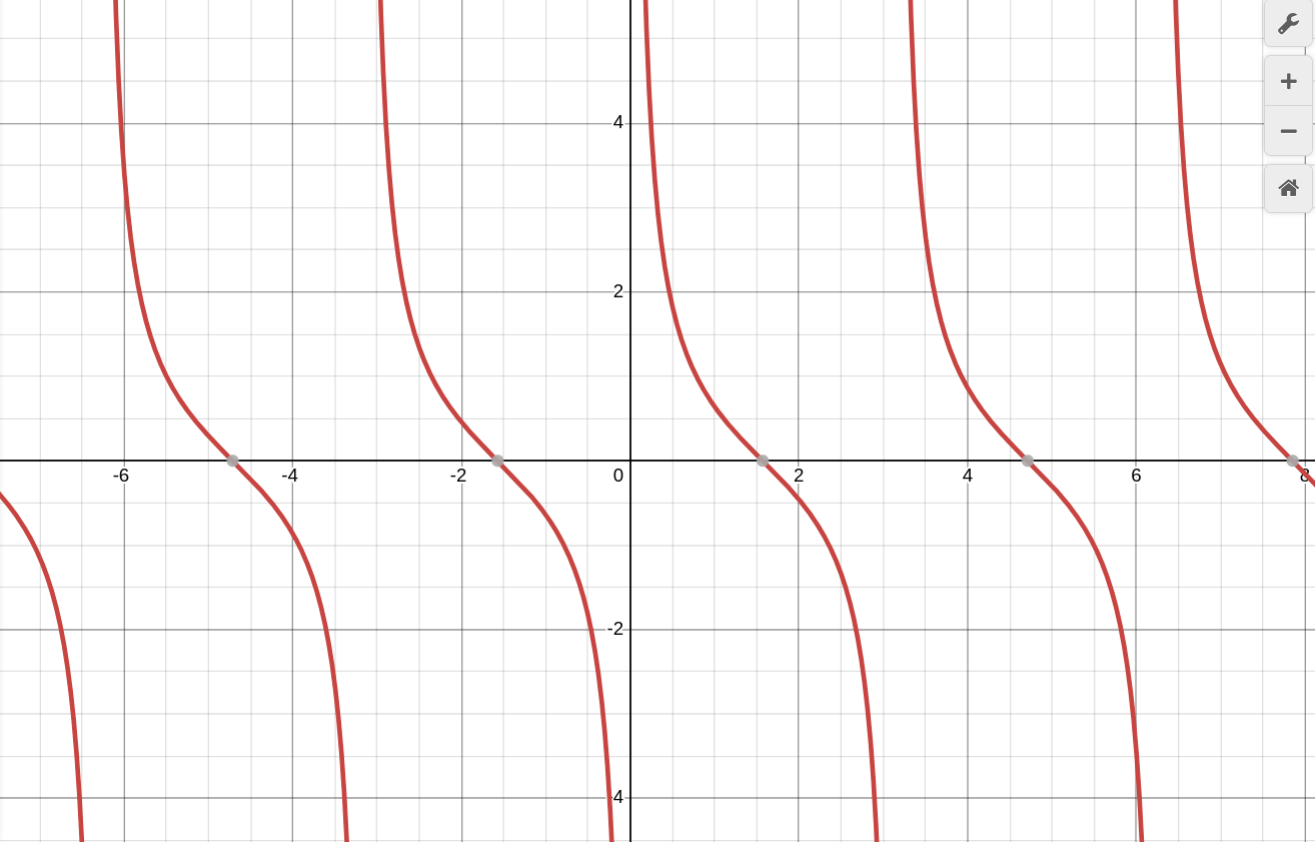
Свойства:
1. Область определения: x ≠ πk, k ∈ Z
2. Область значений: E(y) = R
3. Функция нечётная: ctg(−x) = −ctg x
4. Функция периодическая с периодом π
5. Точки пересечения с осями координат:
Ox: (π/2 + πk; 0), k ∈ Z;
Oy: отсутствуют
6. Промежутки знакопостоянства:
ctg x > 0 при x ∈ (πk; π/2 + πk), k ∈ Z
ctg x < 0 при x ∈ (π/2 + πk; π + πk), k ∈ Z
7. Промежутки возрастания и убывания:
убывает на промежутках x ∈ (πk; π + πk), k ∈ Z
8. Максимумы и минимумы: отсутствуют
Секанс
Уравнение y = sec x, график - секансоидa
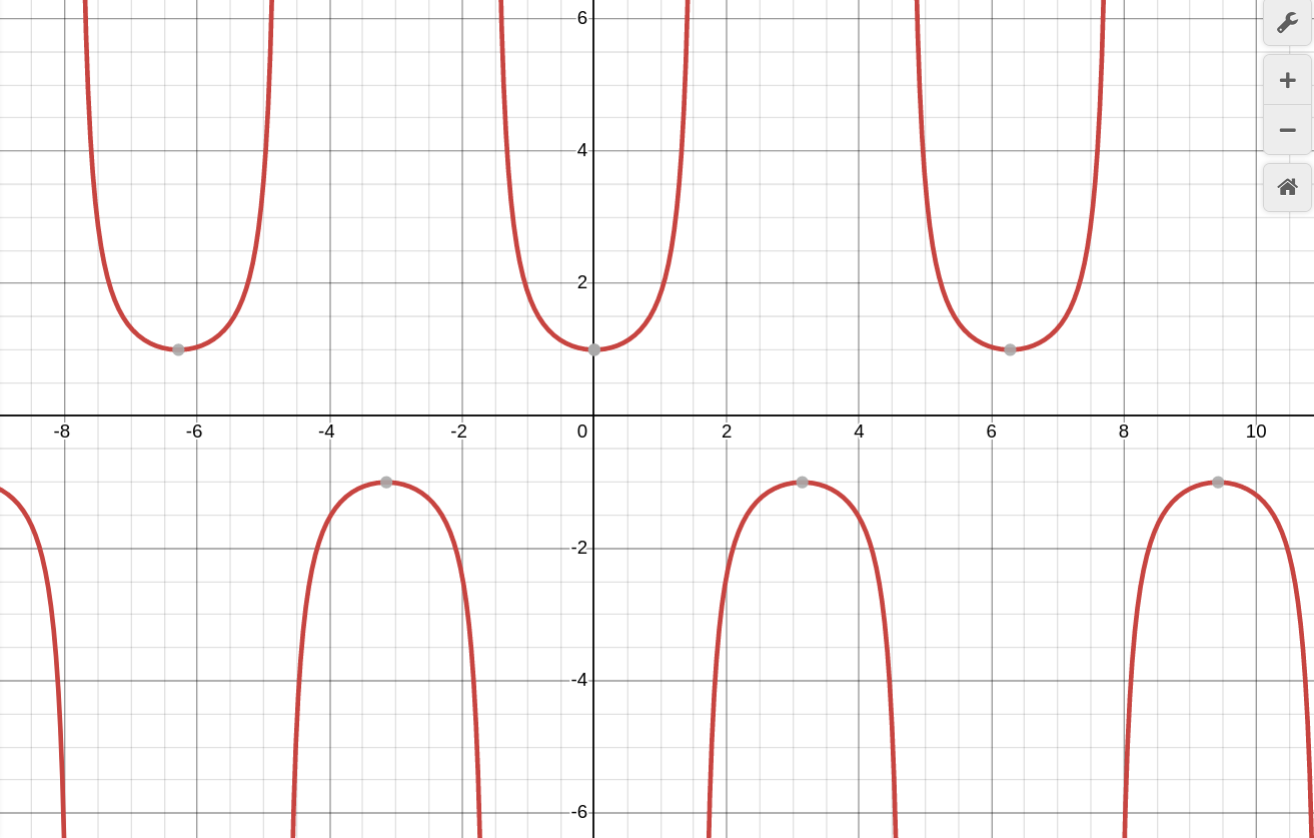
Свойства:
1. Область определения: x ≠ π/2 + πk, k ∈ Z
2. Область значений: E(y) = (−∞; −1] ∪ [1; +∞)
3. Функция чётная: sec(−x) = sec x
4. Функция периодическая с периодом 2π
5. Точки пересечения с осями координат:
Ox: отсутствуют
Oy: (0; 1)
6. Промежутки знакопостоянства:
sec x > 0 при x ∈ (−π/2 + 2πk; π/2 + 2πk), k ∈ Z
sec x < 0 при x ∈ (π/2 + 2πk; 3π/2 + 2πk), k ∈ Z
7. Промежутки возрастания и убывания:
убывает на x ∈ [π + 2πk; 3π/2 + 2πk) ∪ (3π/2 + 2πk; 2π + 2πk], k ∈ Z
возрастает на x ∈ [2πk; π/2 + 2πk) ∪ (π/2 + 2πk; π + 2πk], k ∈ Z
8. Максимумы и минимумы:
xmin = 2πk, k ∈ Z
xmax = π + 2πk, k ∈ Z
Косеканс
y = cosec x
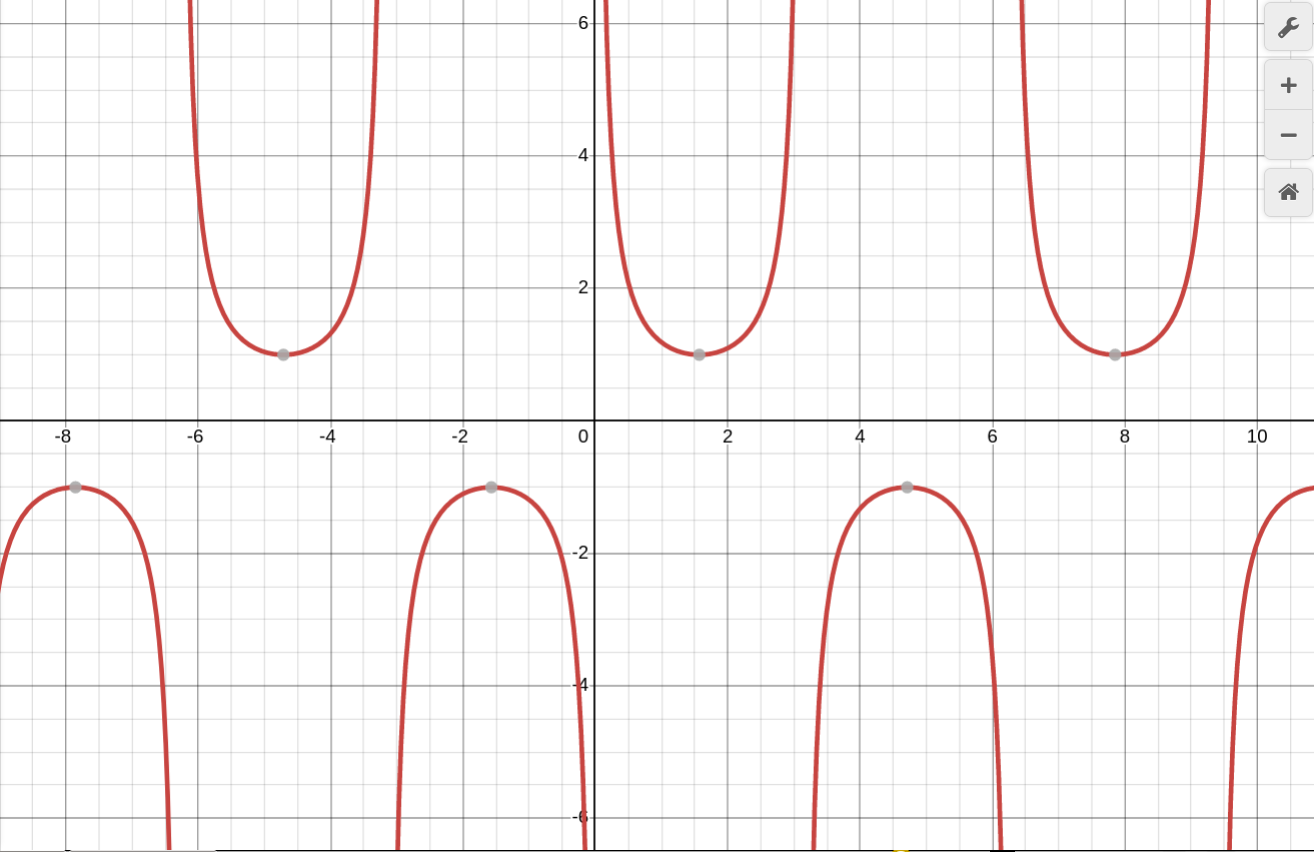
Свойства:
1. Область определения: x ≠ πk, k ∈ Z
2. Область значений: E(y) = (−∞; −1] ∪ [1; +∞)
3. Функция нечётная: cosec(−x) = −cosec x
4. Функция периодическая с периодом 2π
5. Точки пересечения с осями координат: отсутствуют
6. Промежутки знакопостоянства:
cosec x > 0 при x ∈ (2πk; π + 2πk), k ∈ Z
cosec x < 0 при x ∈ (π + 2πk; 2π + πk), k ∈ Z
7. Промежутки возрастания и убывания:
убывает на x ∈ [−π/2 + 2πk; 2πk) ∪ (2πk; π/2 + 2πk], k ∈ Z
возрастает на x ∈ [π/2 + 2πk; π + πk) ∪ (π + 2πk; 3π/2 + 2πk], k ∈ Z
8. Максимумы и минимумы:
xmin = π/2 + 2πk, k ∈ Z
xmax = 3π/2 + 2πk, k ∈ Z