Степенная функция y = x^a

Степенная функция y = x ^a, где a (показатель степени) — некоторое вещественное число

Натуральные показатели

Показатель a = 2n — чётное натуральное число

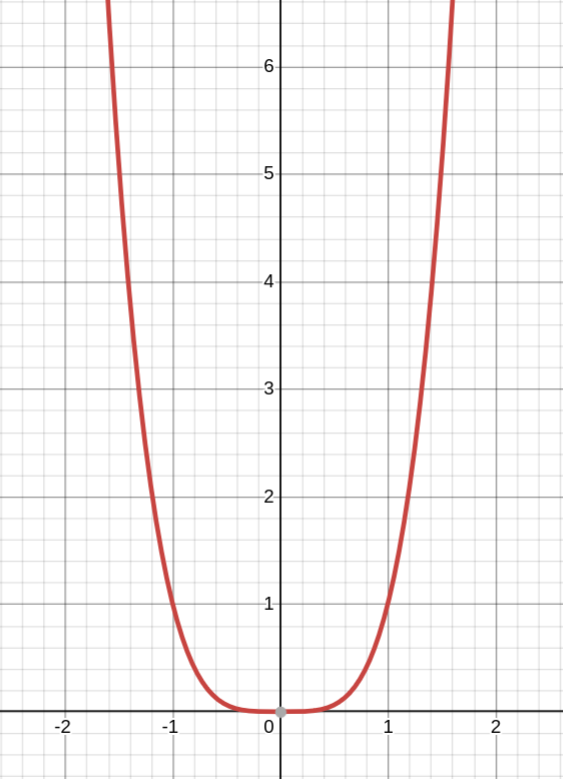
1. Область определения — все действительные числа (D(y) = R)

2. Область значений — неотрицательные числа (y ≥ 0)

3. Функция чётная

4. Функция убывает на промежутке x ≤ 0 и возрастает на промежутке x ≥ 0

5. Промежутки знакопостоянства: y > 0 при x ∈ (−∞; 0) ∪ (0; +∞)

Показатель a = 2n − 1 — нечётное натуральное число

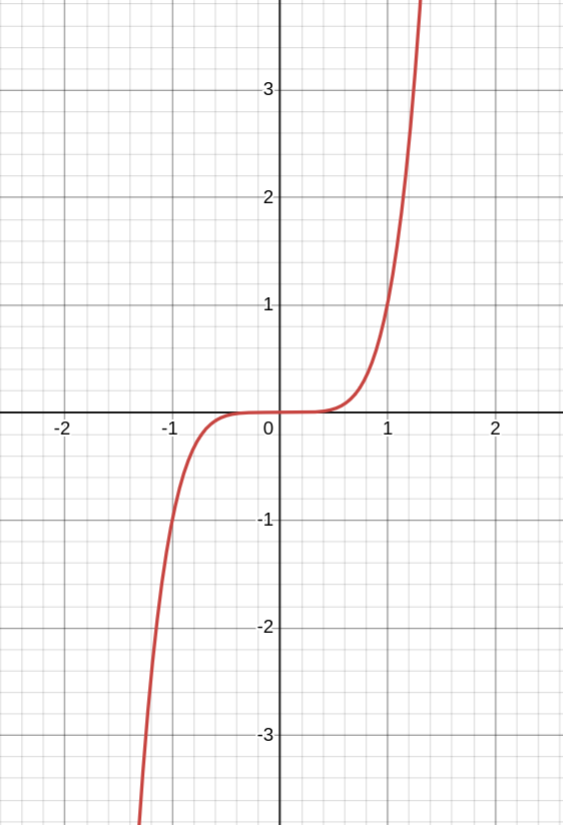
1. Область определения — все действительные числа (D(y) = R)

2. Область значений — все действительные числа (E(y) = R)

3. Функция нечётная

4. Функция возрастает на всей действительной оси

5. Промежутки знакопостоянства: y < 0 при x ∈ (−∞; 0); y > 0 при x ∈ (0; +∞)

Целые отрицательные показатели

Сводится к виду: y = x⁻ⁿ = $\frac{1}{x^n}$

Показатель a = −2n − чётное отрицательное число (n — натуральное число)

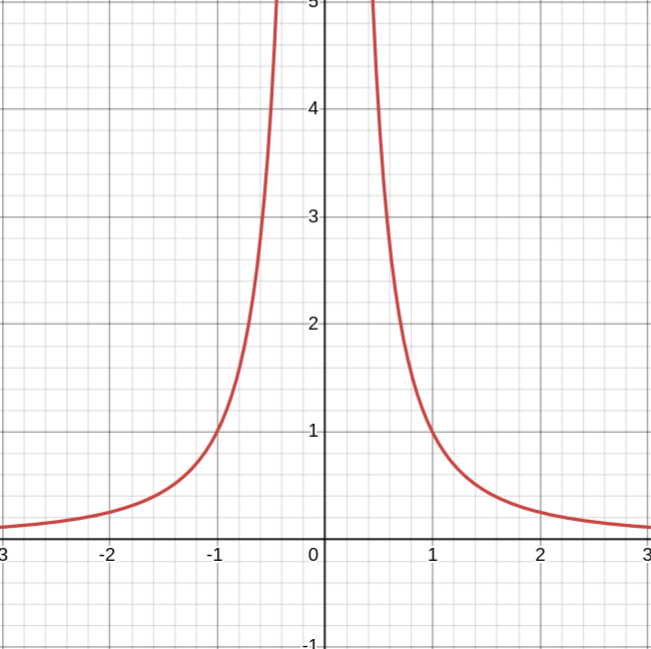
1. Область определения — все действительные числа, кроме x = 0 (D(y) = (−∞; 0) ∪ (0; +∞))

2. Область значений — положительные числа (y > 0)

3. Функция чётная

4. Функция возрастает на промежутке x < 0 и убывает на промежутке x > 0

5. Промежутки знакопостоянства: y > 0 при x ∈ (−∞; 0) ∪ (0; +∞)

Показатель a = −(2n − 1) − нечётное отрицательное число (n — натуральное число)

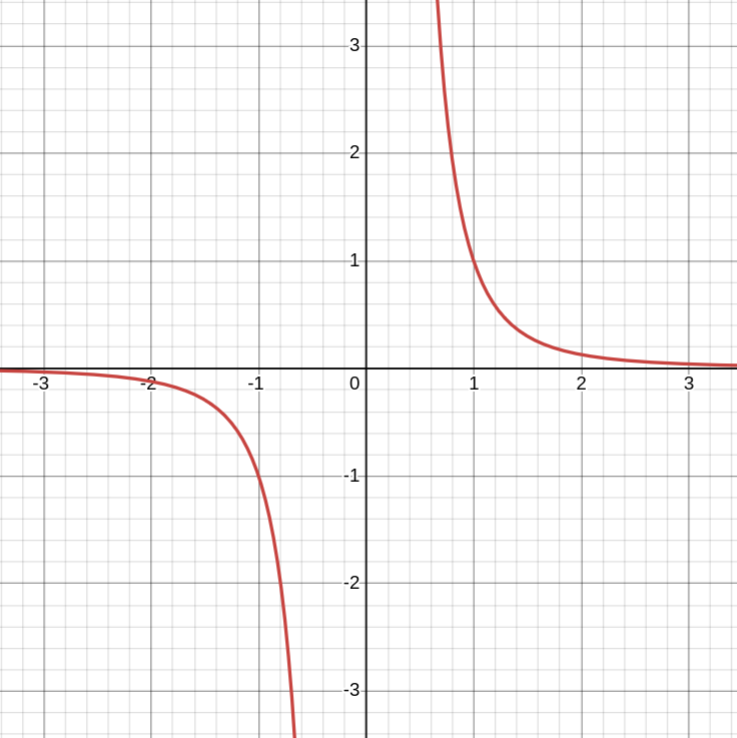
1. Область определения — все действительные числа, кроме x = 0 (D(y) = (−∞; 0) ∪ (0; +∞))

2. Область значений — все действительные числа, кроме y = 0 (E(y) = (−∞; 0) ∪ (0; +∞))

3. Функция нечётная

4. Функция убывает на промежутках x < 0 и x > 0

5. Промежутки знакопостоянства: y < 0 при x ∈ (−∞; 0); y > 0 при x ∈ (0; +∞)

Нецелые положительные показатели

Сводится к виду: $y=x^{\frac{p}{q}}=\sqrt[q]{x^p}$

Показатель a = p/q — положительное действительное нецелое число, q — чётное

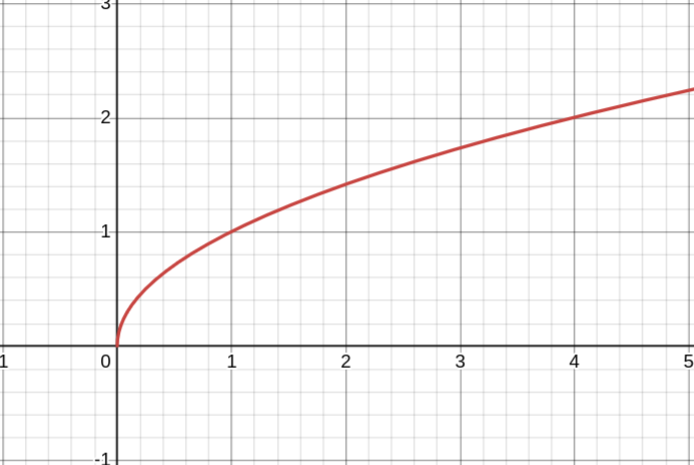
1. Область определения — неотрицательные числа (D(y) = [0; +∞))

2. Область значений — неотрицательные числа (E(y) = [0; +∞))

3. Функция ни чётная, ни нечётная

4. Функция возрастает на промежутке x ≥ 0

5. Промежутки знакопостоянства: y > 0 при x ∈ (0; +∞)

Показатель a = p/q — положительное действительное нецелое число, q — нечётное

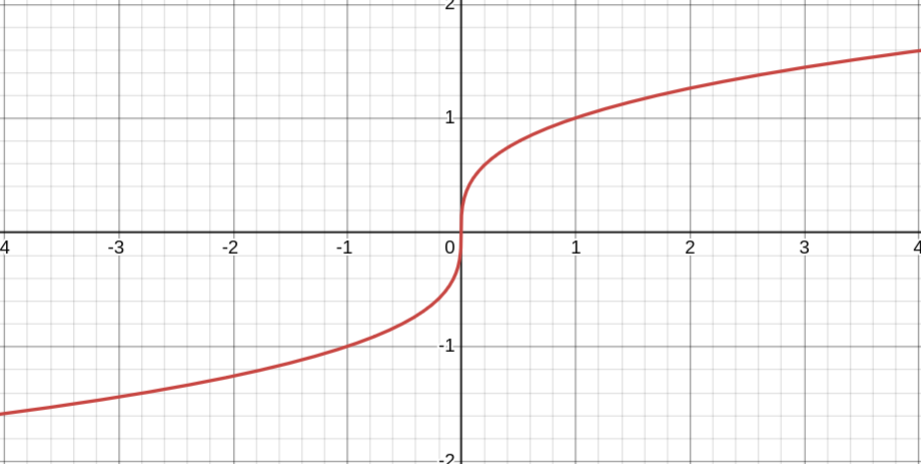
1. Область определения — все действительные числа (D(y) = R)

2. Область значений — все действительные числа (E(y) = R)

3. Функция нечётная

4. Функция возрастает на всей действительной оси

5. Промежутки знакопостоянства: y < 0 при x ∈ (−∞; 0); y > 0 при x ∈ (0; +∞)

Нецелые отрицательные показатели

Сводится к виду: $y=x^{-\frac{p}{q}}=\frac{1}{\sqrt[q]{x^p}}$

Показатель a = −p/q — отрицательное действительное нецелое число, q — чётное

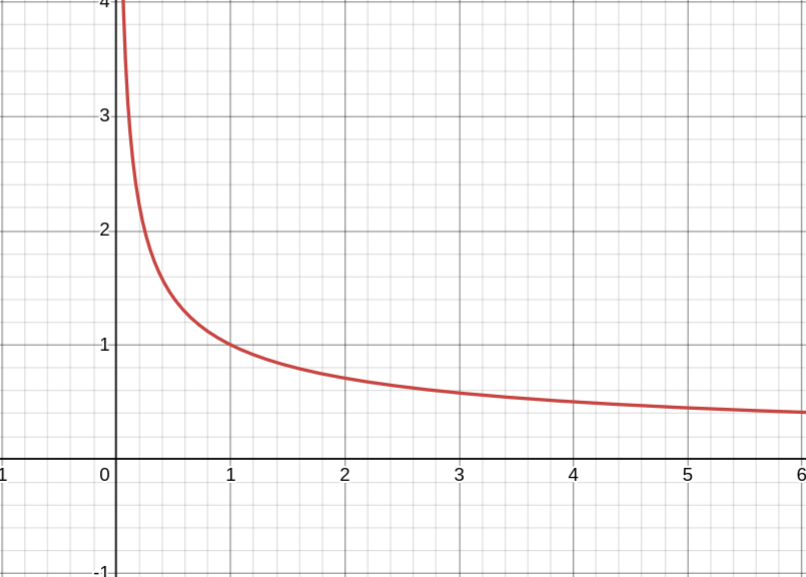
1. Область определения — положительные числа (D(y) = (0; +∞))

2. Область значений — положительные числа (E(y) = (0; +∞))

3. Функция ни чётная, ни нечётная

4. Функция убывает на промежутке x > 0

5. Промежутки знакопостоянства: y > 0 при x ∈ (0; +∞)

Показатель a = −p/q — отрицательное действительное нецелое число, q — нечётное

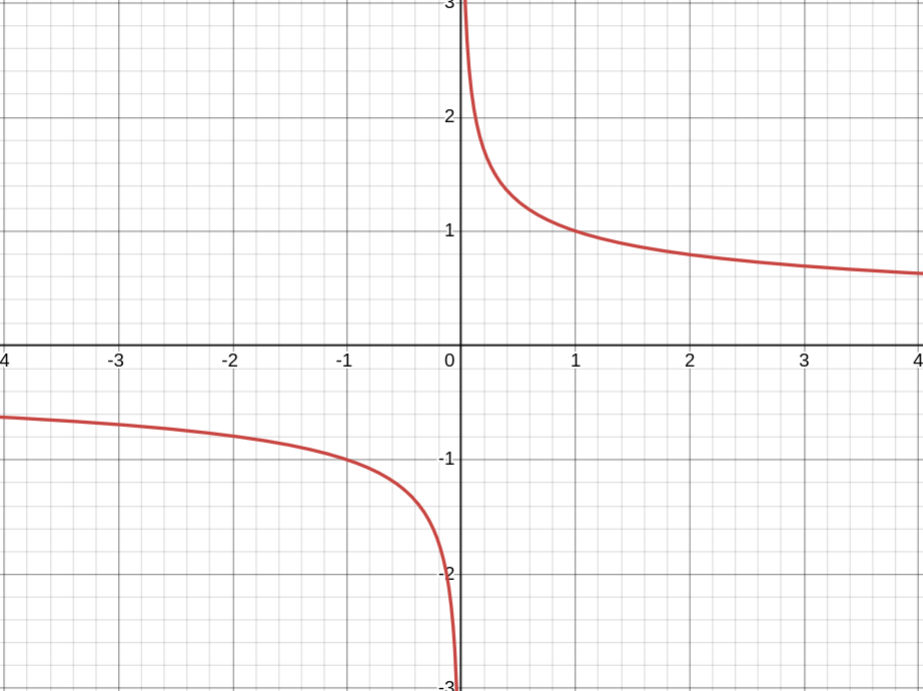
1. Область определения — все действительные числа, кроме x = 0 (D(y) = (−∞; 0) ∪ (0; +∞))

2. Область значений — все действительные числа, кроме x = 0 (D(y) = (−∞; 0) ∪ (0; +∞))

3. Функция нечётная

4. Функция убывает на промежутках x < 0 и x > 0

5. Промежутки знакопостоянства: y < 0 при x ∈ (−∞; 0); y > 0 при x ∈ (0; +∞)