Функции

Содержание

• Смещение, сжатие, растяжение
• Исследование функций
• Примеры исследования функций

y = f(x)

y = C f (ax + b) + D

Коэффициент a

При a < 0 график функции зеркально отражается относительно оси Oy.

При |a| < 1 происходит растяжение по оси Ox.

При |a| > 1 происходит сжатие по оси Ox.

Коэффициент b

При b > 0 график смещается по оси Ox влево на b единиц.

При b < 0 график смещается по оси Ox вправо на b единиц.

Коэффициент C

При C < 0 график функции зеркально отражается относительно оси Ox.

При |C | < 1 происходит сжатие по оси Oy.

При |C | > 1 происходит растяжение по оси Oy.

Коэффициент D

При D > 0 график смещается по оси Oy вверх на D единиц.

При D < 0 график смещается по оси Oy вниз на D единиц.

Уравнение: y = f(x)

Список свойств:

1. Область определения функции
2. Область значений функции
3. Точки экстремума, минимума и максимума
4. Промежутки возрастания и убывания (монотонности) функции
5. Наибольшее и наименьшее значения функции
6. Пересечение с осями координат, нули функции
7. Промежутки знакопостоянства
8. Чётность функции
9. Периодичность функции
10. Непрерывность функции*
11. Ограниченность функции*
12. Точки перегиба, промежутки выпуклости*
13. Поведение на бесконечности, горизонтальные или наклонные асимптоты*

(Звёздочками * обозначены свойства, не исследуемые в школьном курсе алгебры.)

Область определения функции

Область определения функции - множество значений x, на котором задаётся функция.

Обозначается D(y)

Область значений функции

Область значений функции - множество, состоящее из всех значений, которые принимает функция (значения y).

Обозначается E(y)

Определить область значений можно после вычисления максимальных и минимальных значений функции.

Точки экстремума, минимума и максимума

Экстремум — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

В точках экстремума производная функции равна нулю: f ′(x) = 0.

Чтобы определить, является ли точка экстремума x₀ точкой максимума или минимума, нужно исследовать поведение функции в окрестности этой точки.

Для точки максимума (x_max) функция перед ней возрастает, после точки - убывает: x₁ < x₀ < x₂; f ′(x₁) > 0; f ′(x₂) < 0.

Для точки минимума (x_min) функция перед ней убывает, после точки - возрастает: x₁ < x₀ < x₂; f ′(x₁) < 0; f ′(x₂) > 0.

Если производная не существует в какой-либо точке, то это говорит о том, что в этой точке либо разрыв функции, либо резкий излом, либо касательная проходит вертикально.

Промежутки возрастания и убывания (монотонности) функции

Функция y = f(x) возрастает на неком промежутке, если для x₂ > x₁ выполняется условие y₂ > y₁. На данном промежутке производная функции f ′(x) > 0.

Функция y = f(x) убывает на неком промежутке, если для x₂ > x₁ выполняется условие y₂ < y₁. На данном промежутке производная функции f ′(x) < 0.

Пусть у производной функции f ′(x) нулями и точками разрыва являются x₁, x₂, x₃, ..., x_n. Тогда нужно вычислить значение производной функции в промежутках между этими точками (определить знак производной):

x :	(−∞; x1)	x1	(x1; x2)	x2	(x2; x3)	x3	...	xn	(xn; +∞)
f ′(x) :	+	0	−	0	+	0	...	0	+
f(x) :	🡕	max	🡖	min	🡕	-	...	-	🡕

Наибольшее и наименьшее значения функции

Наибольшее значение функции: y_max = f (x_max).

Наименьшее значение функции: y_min = f (x_min).

Пересечение с осями координат, нули функции

Чтобы найти пересечение с осью абсцисс Ox (нули функции), её нужно приравнять к нулю: f (x) = 0 и найти корни данного уравнения.

Чтобы найти пересечение с осью ординат Oy, нужно подставить точку x = 0: y = f (0).

Промежутки знакопостоянства

Метод интервалов:

Пусть у функции f(x) нулями и точками разрыва являются x₁, x₂, ..., x_n. Тогда нужно вычислить значение функции в промежутках между этими точками (определить знак функции):

x :	(−∞; x1)	x1	(x1; x2)	x2	...	xn	(xn; +∞)
f(x) :	+	0	−	0	...	0	+

Чётность функции

Чётная функция: f (−x) = f (x). График симметричен относительно оси Oy.

Нечётная функция: f (−x) = −f (x). График симметричен относительно начала координат - точки O(0; 0).

Ни чётная, ни нечётная функция: не выполняется ни одно из предыдущих условий.

(Функция y = 0 является одновременно и чётной, и нечётной).

Периодичность функции

Периодическая функция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (периода функции T) на всей области определения.

f (x) = f (x + nT), где n ∈ Z

Непрерывность функции

Непрерывная функция — функция, которая меняется без мгновенных «скачков» (называемых разрывами), то есть такая, малые изменения аргумента которой приводят к малым изменениям значения функции.

$\underset{x\to x_0}{\lim }f\left(x\right)=f\left(x_0\right)$

Ограниченность функции

Функция ограниченная сверху: существует такое число M, что для всех x из рассматриваемого множества выполняется f(x) < M.

Функция ограниченная снизу: существует такое число m, что для всех x из рассматриваемого множества выполняется f(x) > m.

Точки перегиба, промежутки выпуклости

Чтобы найти точки перегиба, нужно найти вторую производную и приравнять её к нулю: f ′′(x) = 0.

Поведение на бесконечности, горизонтальные или наклонные асимптоты

Формулы нахождения асимптот

Исследовать функцию y = x² + x − 6 и построить её график

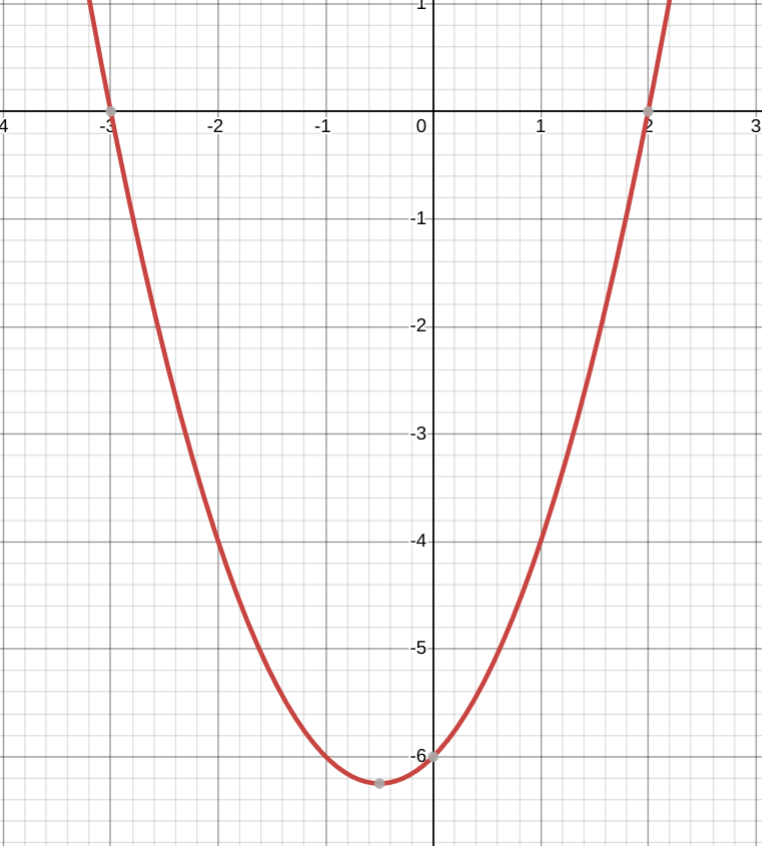
1. D(y) = R

2. E(y) ∈ [−6,25; +∞)

3. y ′ = 2x + 1
2x + 1 = 0
x = −0,5 - точка экстремума
При x < −0,5 y ′ < 0
При x > −0,5 y ′ > 0
=> x = −0,5 - точка минимума

4. При x < −0,5: y ′ < 0 - функция убывает
При x > −0,5: y ′ > 0 - функция возрастает

5. Наименьшее значение достигается в точке минимума: y(−0,5) = (−0,5)² + (−0,5) − 6 = −6,25
Наибольшего значения нет (стремится к бесконечности)

6. Пересечение с осью Oy: y(0) = 0² + 0 − 6 = −6 => точка (0; −6)
Пересечения с осью Ox:
x² + x − 6 = 0
x₁ = −3; x₂ = 2 => точки (−3; 0), (2; 0)

7. Промежутки знакопостоянства:

x:	(−∞; −3)	−3	(−3; 2)	2	(2; +∞)
y:	+	0	−	0	+

Таким образом, f(x) > 0 при x ∈ (−∞; −3) ∪ (2; +∞)
f(x) < 0 при x ∈ (−3; 2)

8. Функция ни чётная, ни нечётная.

9. Функция не периодическая.

Исследовать функцию $y=\frac{x}{x^2-1}$ и построить её график

1. D(y) = (−∞; −1) ∪ (−1; 1) ∪ (1; +∞)

2. E(y) ∈ (−∞; +∞)

3. y ′ = $-\frac{x^2+1}{x^4-2x^2+1}$
Корней нет => точек экстремума нет, точки разрыва x = −1 и x = 1.

4. При x < −1: y ′ < 0 - функция убывает
При x ∈ (−1; 1): y ′ < 0 - функция убывает
При x > 1: y ′ < 0 - функция убывает

5. Наибольшее и наименьшее значения функции отсутствуют.

6. Пересечение с осями координат: (0; 0)

7. Промежутки знакопостоянства:

x:	(−∞; −1)	−1	(−1; 0)	0	(0; 1)	1	(1; +∞)
y:	−	−∞	+	0	−	+∞	+

8. Функция чётная.

9. Функция не периодическая.