Показательная и логарифмическая функции

Содержание

Показательная функция y = a^x, где a — основание, некоторое неотрицательное число, a ≠ 1.

a > 1

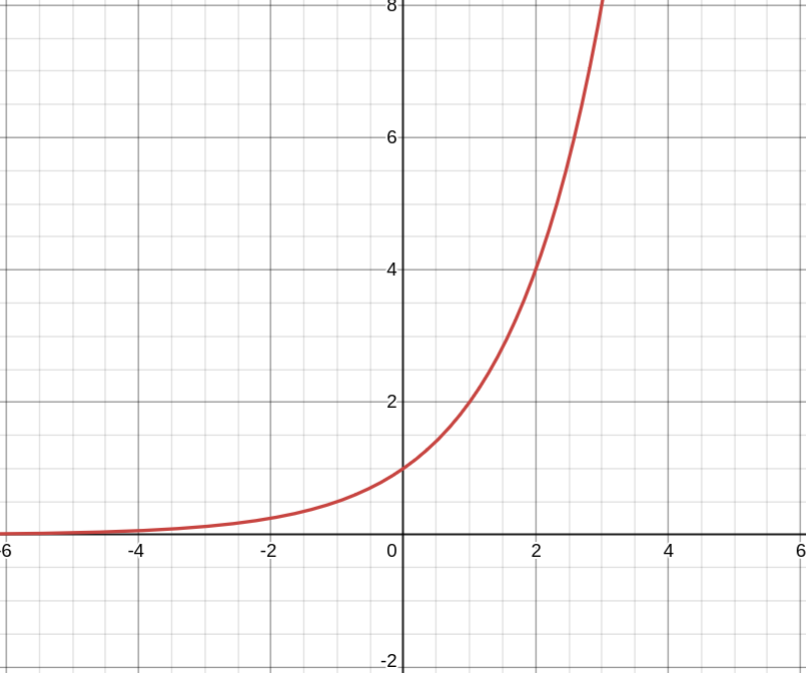
1. Область определения — все действительные числа: D(y) = R

2. Область значений — положительные числа: E(y) ∈ (0; +∞)

3. Функция ни чётная, ни нечётная

4. Функция возрастает на всей действительной прямой

5. Точки пересечения с осями координат: Oy: (0; 1)

6. Экстремумов нет

0 < a < 1

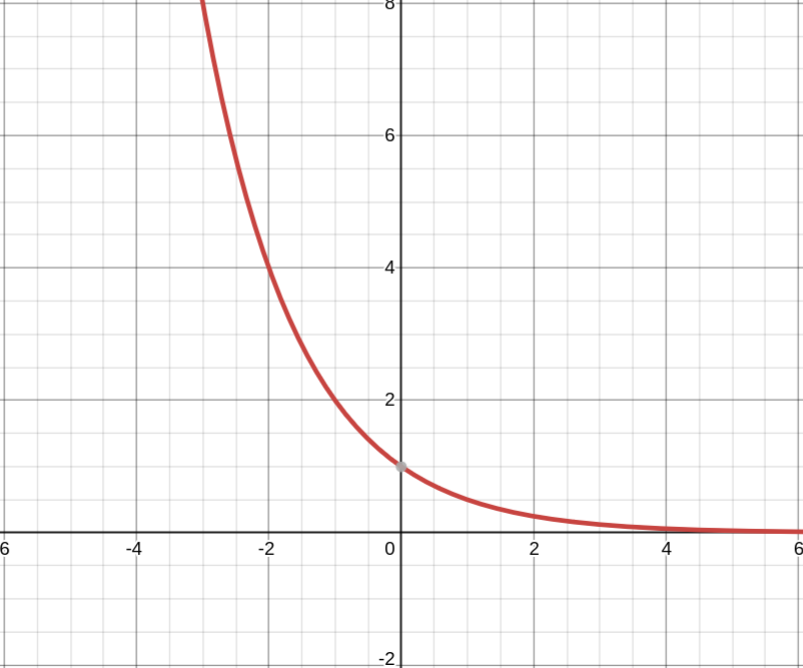
1. Область определения — все действительные числа (D(y) = R)

2. Область значений — положительные числа: E(y) ∈ (0; +∞)

3. Функция ни чётная, ни нечётная

4. Функция убывает на всей действительной прямой

5. Точки пересечения с осями координат: Oy: (0; 1)

6. Экстремумов нет

Смещение, сжатие, растяжение

y = b · a^x + c

Если b > 1, график растянут по оси Oy, 0 < b < 1, график сжат по оси Oy, b < 0, график отражён относительно оси Ox.

Если c > 0, то пересечение с осью Oy выше точки (0; 1), если c < 0 то пересечение с Oy лежит ниже точки (0; 1).

Показательные неравенства

Неравенство нужно привести к виду:

a^x > a^b (a^x < a^b)

Если основание a > 1, то знак неравенства сохраняется при переходе к показателю:

x > b (x < b)

Если основание 0 < a < 1, то знак неравенства меняется на противоположный при переходе к показателю:

x < b (x > b)

Примеры

16^x − 17 · 4^x + 16 ≤ 0

(4^x)² − 17 · 4^x + 16 ≤ 0

Замена: 4^x = t

t ² − 17t + 16 ≤ 0

Нули функции: t₁ = 1, t₂ = 16

Обратная замена:

4^x = 1 => x₁ = 0

4^x = 16 => x₂ = 2

Логарифмическая функция y = log_ax, где a — основание, некоторое неотрицательное число, a ≠ 1, x > 0.

Является обратной для показательной функции.

a > 1

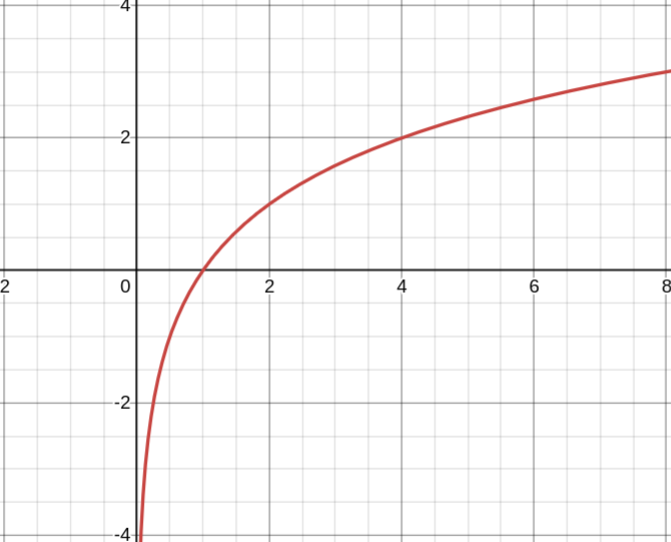
1. Область определения — положительные числа: D(y) ∈ (0; +∞)

2. Область значений — все действительные числа: E(y) = R

3. Функция ни чётная, ни нечётная

4. Функция возрастает на всей области определения

5. Точки пересечения с осями координат: Ox: (1; 0)

6. Экстремумов нет

0 < a < 1

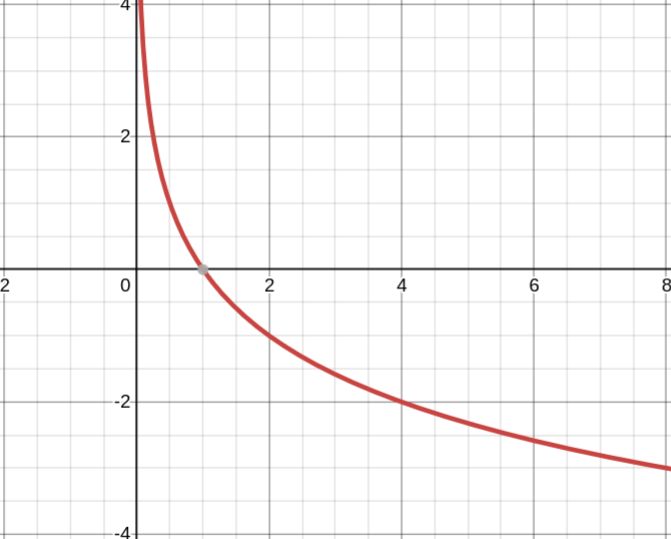
1. Область определения — положительные числа: D(y) ∈ (0; +∞)

2. Область значений — все действительные числа (E(y) = R)

3. Функция ни чётная, ни нечётная

4. Функция убывает на всей области определения

5. Точки пересечения с осями координат: Ox: (1; 0)

6. Экстремумов нет

Смещение, сжатие, растяжение

y = D log_a(bx + c) + E

При a > 1 чем больше основание a, тем более сжат график по оси Oy. При a < 1 чем меньше основание a, тем более сжат график по оси Oy.

Если b > 1, график сжат по оси Ox; 0 < b < 1, график растянут по оси Ox; b < 0, график отражён относительно оси Oy (чем больше модуль b, тем сильнее сжат график).

Если c > 0, то смещение влево по оси Ox; если c < 0 то смещение по Ox вправо.

При D < 0 график отражён по оси Oy; при |D| > 1 - растяжение по оси Oy; |D| < 1 - сжатие по Oy.

Если E > 0, то график смещён вверх по оси Oy; если E < 0, то вниз по Oy.

Логарифмические неравенства

Неравенство нужно привести к виду:

log_ax > log_ab (log_ax < log_ab)

Если основание a > 1, то знак неравенства сохраняется при переходе к показателю:

x > b (x < b)

Если основание 0 < a < 1, то знак неравенства меняется на противоположный при переходе к показателю:

x < b (x > b)